13. RNN (part b)
16 RNN B V4 Final
As we've see, in FFNN the output at any time t, is a function of the current input and the weights. This can be easily expressed using the following equation:
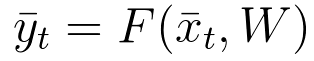
Equation 28
In RNNs, our output at time t, depends not only on the current input and the weight, but also on previous inputs. In this case the output at time t will be defined as:
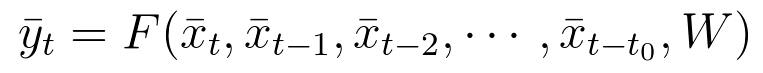
Equation 29
This is the RNN folded model:
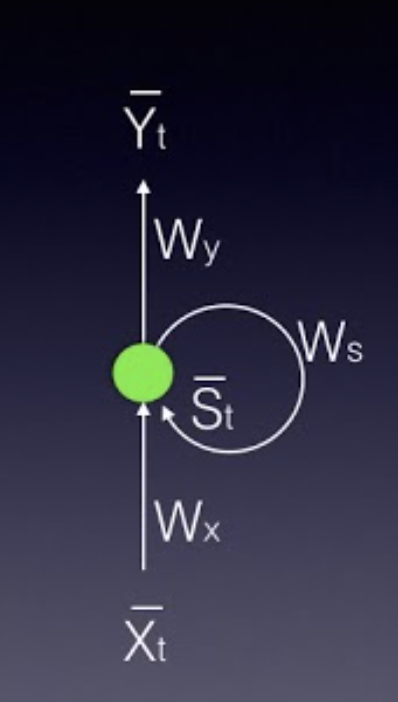
The RNN folded model
In this picture, \bar{x} represents the input vector, \bar{y} represents the output vector and \bar{s} denotes the state vector.
W_x is the weight matrix connecting the inputs to the state layer.
W_y is the weight matrix connecting the state layer to the output layer.
W_s represents the weight matrix connecting the state from the previous timestep to the state in the current timestep.
The model can also be "unfolded in time". The unfolded model is usually what we use when working with RNNs.
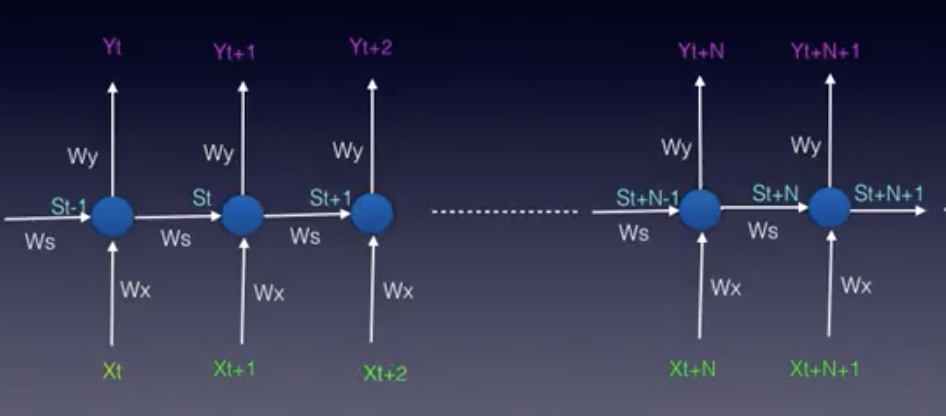
The RNN unfolded model
In both the folded and unfolded models shown above the following notation is used:
\bar{x} represents the input vector, \bar{y} represents the output vector and \bar{s} represents the state vector.
W_x is the weight matrix connecting the inputs to the state layer.
W_y is the weight matrix connecting the state layer to the output layer.
W_s represents the weight matrix connecting the state from the previous timestep to the state in the current timestep.
In FFNNs the hidden layer depended only on the current inputs and weights, as well as on an activation function \Phi in the following way:
\bar{h}=\Phi(\bar{x}W).
Equation 30
In RNNs the state layer depended on the current inputs, their corresponding weights, the activation function and also on the previous state:
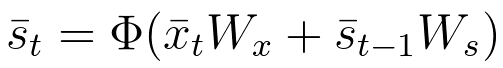
Equation 31
The output vector is calculated exactly the same as in FFNNs. It can be a linear combination of the inputs to each output node with the corresponding weight matrix W_y, or a softmax function of the same linear combination.
\bar{y}_t=\bar{s}_t W_y
or
\bar{y}_t=\sigma(\bar{s}_t W_y)
Equation 32
The next video will focus on the unfolded model as we try to further understand it.